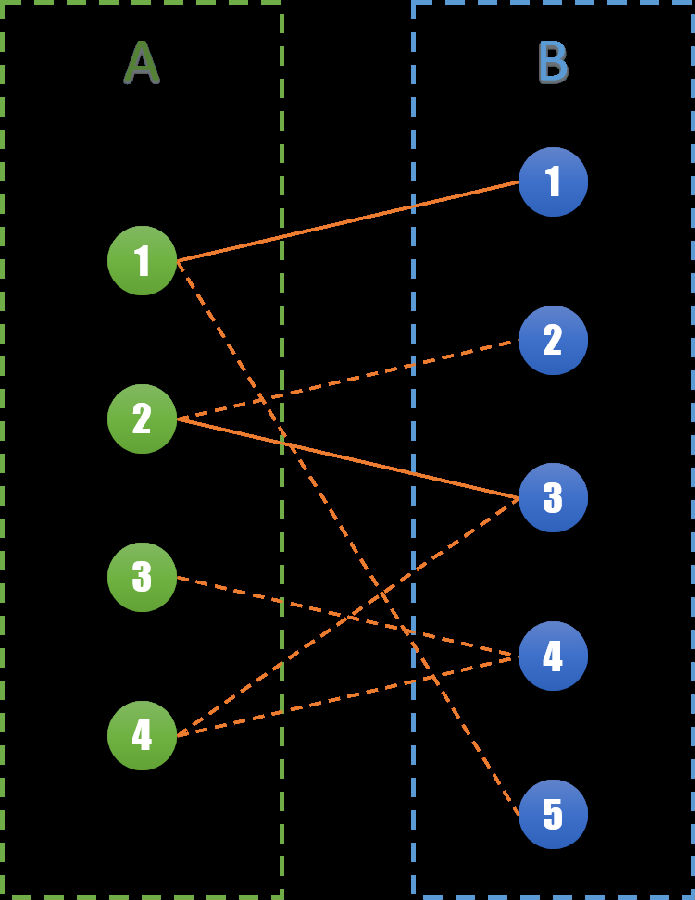
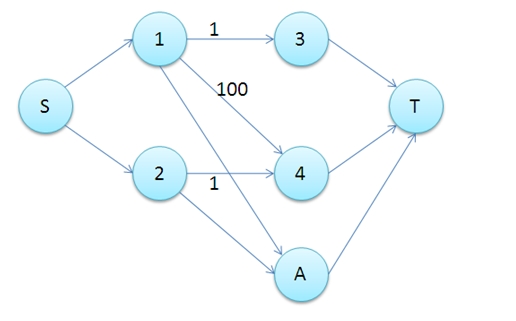
#78 二分图最大匹配 从前一个和谐的班级,有 n l 个是男生,有 n r 个是女生。 编号分别为 1, , n l 和 1, , n r 。 有若干个这样的条件:第 v 个男生和第 u 个女生愿意结为配偶。 请问这个班级里最多产生多少对配偶?可以将求二分图最大匹配的问题转化为最 大流的问题。 增加两个顶点s、t。对于x中的每个顶点xi, 连边(s, xi),容量为1。对于y中的每个顶 点yj,连边(yj, t),容量为1。对于原图中 的边(xi, yj),将容量设为1。显而易见,s 到t的最大流就是原图的最大匹配。 ? · 二分图最大权匹配 从前一个和谐的班级,有 n l 个是男生,有 n r 个是女生。 编号分别为 1, , n l 和 1, , n r 。 有若干个这样的条件:第 v 个男生和第 u 个女生愿意结为配偶,且结为配偶后幸福程度为 w 。 请问这个班级里幸福程度之和最大是多少?
Hihocoder1122 二分图二 二分图最大匹配之匈牙利算法 太傅博客
二分图最大匹配 python
二分图最大匹配 python- · 二分图二•二分图最大匹配之匈牙利算法 上一回我们已经将所有有问题的相亲情况表剔除了,那么接下来要做的就是安排相亲了。 因为过年时间并不是很长,所以姑姑希望能够尽可能在一天安排比较多的相亲。 由于一个人同一天只能和一个人相亲,所以要 从 · 二分图的最大匹配 (匈牙利算法) End 1637 PDT Ended Please login with your account first



蒟蒻图论 二分图匹配 蒟蒻のblog
这篇将 二分图最大匹配 转换成 最大流问题 的思维过程,想必会让你对图算法又了新的认识。 算法题目的考察从广义上来讲,就是在考察你 是否能将这个问题对应到一个你熟悉的求解模型和方法上 ,如果你抽象得当,你就可以利用已有的算法,去高效的求解07 · 二分图的最大匹配算法,其实就是要找出二分图中一个最大的匹配。那么什么是二分图中的匹配?二分图的匹配本质上是一个集合g',也就是一个原本二分图g的子集。对于g' = (v,e),任取其中的两条边,这两条边关联的顶点是不重合的,就可以说这个二分图g的子集是它的一个匹配。比如下面的目录 1 问题描述 2 解决方案 1 问题描述 何为二分图的最大匹配问题? 引用自百度百科: 首先得说明一下何为匹配: 给定一个 二分图 G ,在 G 的一个子图 M 中, M 的边集 {E} 中的任意两条边都不依附于同一个顶点,则称 M 是一个 匹配 。 极大匹配 (Maximal Matching) 是指在当前已完成的匹配下, 无法再
· 二分图匹配及其应用 一、 二分图基本概念 1 二分图:无向图G的顶点集V分成两部分x和y,G中每条边的两个端点一定是一个属于x而另一个属于y,因此二分图可简记为G=(x,y,E) ,西西软件园最安全的下载资讯站。 · 这个题很明显是一个二分图的最大匹配问题(不要问我怎么看出来的),所以既可以用匈牙利算法解(代码 One),也可以使用构建网络流模型来解(代码 Two)。 匈牙利的问题就不多说了,裸算法,(0级题都是裸算法模版题),而这里如果用网络流模型来解,就涉及到了一个建图的问题,首先我们先建立一个超级源点通向外籍飞行员,权值为 1 ,接着建立一个超级给定一张二分图,左右部均有 $n$ 个点,共有 $m$ 条带权边,且保证有完美匹配。 求一种完美匹配的方案,使得最终匹配边的边权之和最大。 求一种完美匹配的方案,使得最终匹配边的边权之和最大。
· 二分图的最大匹配 (匈牙利算法) ,1、二分图、最大匹配什么是二分图:二分图又称作二部图,是图论中的一种特殊模型。设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(iinA,jinB),则称图G为一个二分图。0711 · 二分图判断以及二分图最大匹配 概念 二分图又称作二部图 ,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。 · 在原二分图中删去A、B中均不出现的边,可能剩下单个点、环、路,这可用于表示两个匹配之间的差异。 单个点是不用考虑的,找到所有的路和环就找到了所有其他最大匹配。 寻找环:环中每一个点都是匹配点。 从一个匹配点开始宽度优先搜索,一层列出在




二分图的最大匹配 匈牙利算法 六天 Csdn博客 匈牙利算法伪代码



二分图的最大匹配 完美匹配和匈牙利算法 Yuanda S Blog
· 算法导论——二分图最大匹配 二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。二分图最大匹配 知识点学习 二分图简介二分图即一个无向图,可以把节点分为两个集合,使得同一个集合内的点之间没有边。查看全部 更多练习 你已通过 0/ 7 根据你的目前水平为你推荐以下题目 换一换 难度筛选 一星 二星 三星 四星 五星 变换序列 二分图最大匹配 3星 未练习二分图的最大匹配是指含边最多的匹配。(匹配和最大流问题联系很紧密,事实上关于这两者的问题和算法实在是太多。以后尽量写吧。) 二分图判别: 判断二分图最简单的方法是染色法,有如下定理:一个图是二分图当且仅当可以将其每一个顶点染成红色或蓝色,使任意一条边两端的顶点不同色。 这个定理很容易理解。具体用算法实现时,只需bfs或dfs给图染色检查是否



二分图的最大匹配问题 刘伟的博客 Csdn博客 最大匹配问题



二分匹配的最大流思维 一瓜算法小册
二分图最大权完美匹配(km算法) 321 0704 太难了,蒟蒻只能背模板 二分图最大匹配是寻找最大匹配数,用匈牙利算法。当连接的边带有权值时,要寻找匹配后权值和最大的方案,且保证a集合中的点均有b中的点能匹配。此时问题就转化为二分图最大权完美匹配。二分图的最大匹配算法:设左边集合为A集合,有边集合为B集合。 二分图最大匹配常用的有两种方法。 (1)第一种方法叫做匈牙利算法。 这个方法依次枚举A中的每个点,试图在B集合中找到一个匹配。 对于A集合中一点x,假设B集合中有一个与其相连的点y,若y暂时还没有匹配点,那么x可以和y匹配,找到;否则,设y已经匹配的点为z(显然z是A集合中的一个点),那么 · 二分图最佳带權匹配问题是指在给定带权二分图上求出一个最大匹配的问题,使得所有匹配边权值之和最大。 这个问题也被称为二分图最优匹配。 此类问题通常使用km算法或转换为一个网络费用流问题进行求解。




Ppt 二分图匹配powerpoint Presentation Free Download Id




图论 二分图 北邮微软学生俱乐部
2603 · 所以二分图匹配就是二分图中的匹配 其中,M中的边是匹配边,其他为非匹配边,匹配边的端点叫匹配点,其他为非匹配点。 在常见问题中,经常出现的是求一个二分图的 最大匹配 ,即包含边数最多的边集M。 · 二分图的最大匹配、完美匹配和匈牙利算法 这篇文章讲无权二分图(unweighted bipartite graph)的最大匹配(maximum matching)和完美匹配(perfect matching),以及用于求解匹配的匈牙利算法(Hungarian Algorithm);不讲带权二分图的最佳匹配。 二分图 :简单来说,如果图中点可以被分为两组,并且使得所有边都跨越组的边界,则这就是一个二分图。 准确地说:把一个图的1915 1115 − 一直想用python做一个截图并自动翻译的工具,恰好最近有时间就在网上找了资料,根据资料以及自己的理解做了一个简单的截图翻译工具。 整理一下并把代码放在github给大家参考。界面用python自带的GUI的tkinter,截图用的是pillow,图片识别用的是百度ocr的




通俗易懂小白入门 二分图最大匹配 匈牙利算法



蒟蒻图论 二分图匹配 蒟蒻のblog
二分图最大匹配¶ 详见 二分图最大匹配 页面。 二分图最大权匹配¶ 详见 二分图最大权匹配 页面。 一般图最大匹配¶ 详见 一般图最大匹配 页面。 一般图最大权匹配¶ 详见 一般图最大权匹配 页面。二分图最大匹配问题匈牙利算法 研究了几个小时,终于明白了。 说穿了,就是你从二分图中找出一条路径来,让路径的起点和终点都是还没有匹配过的点,并且路径经过的连线是一条没被匹配、一条已经匹配过,再下一条又没匹配这样交替地出现。 找到这样0711 · HDU1045二分图最大匹配或DFS HDU 1045Fire Net 在地图中有一些障碍物,同一行或同一列不能放置炮台,否则会互相摧毁,除非有障碍物分隔开。 这题范围小,用DFS不难,不过用二分图匹配十分巧妙。而且数据范围大了DFS应该就不行了。



二分图带权匹配km算法与费用流模型建立




Hihocoder1122 二分图二 二分图最大匹配之匈牙利算法 太傅博客
二分图最大匹配的König定理及其证明 06 年 12 月 2 日 / 68 条评论 如果你看不清楚第二个字母,下面有一个大号字体版本: 二分图最大匹配的König定理及其证明 本文将是这一系列里最短的一篇,因为我只打算把König定理证了,其它的废话一概没有。 以下五个问题我可能会在以后的文章里说,如果HNOI13消毒 二分图匹配 二分图最大权匹配 dfs 4星 未练习 109 HNOI14画框 分治 二分图匹配 最小生成树 二分图最大权匹配 3星 未练习 472 ZJOI07矩阵游戏 二分图匹配 二分图最大匹配 3星 未练习 知识点及难度未知的题目更有挑战,如果已准备好,不妨试试 一战到底编程挑战 通过题以上的过程其实就是经典的匈牙利算法,求解二分图的最大匹配问题。 3 匈牙利算法 二分图 定义:设G=(V,E)是一个无向图,顶点集V可分割为两个互不相交的子集X,Y,并且图中每条边关联的两个顶点都分属于这两个互不相交的子集,两个子集内的顶点不相邻。
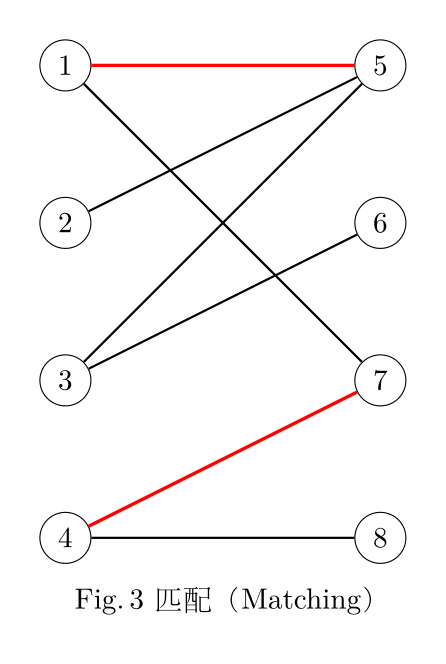



二分图最大匹配问题与匈牙利算法的核心思想 始终



蒟蒻图论 二分图匹配 蒟蒻のblog
求二分图最大匹配可以用最大流或者匈牙利算法。 折叠 最大匹配 给定一个二分图G,在G的一个子图M中,M的边集中的任意两条边都不依附于同一个顶点,则称M是一个匹配 选择这样的边数最大的子集称为图的最大匹配问题(maximal matching problem) 如果一个匹配中,图中的每个顶点都和图中某条边相2710 · 对已经建好的图求最大匹配 Konig定理 最大匹配数=最小覆盖数 二分图的最大独立数 一张残缺的棋盘,用1*2的矩形去覆盖它, 要求矩形不互相重叠 求矩形最多可以放多少个 将棋盘染成黑白相间,黑色方格作为左 边的点,白色方格作为右边的点,相邻 的黑白方格中间连二分图的最大匹配算法 二分图的概念:二分图是图中的一种特殊模型,如果图的顶点v可以分割成两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则该图G成为一个二分图。 二分图如下: 本文通过一个问题来引出
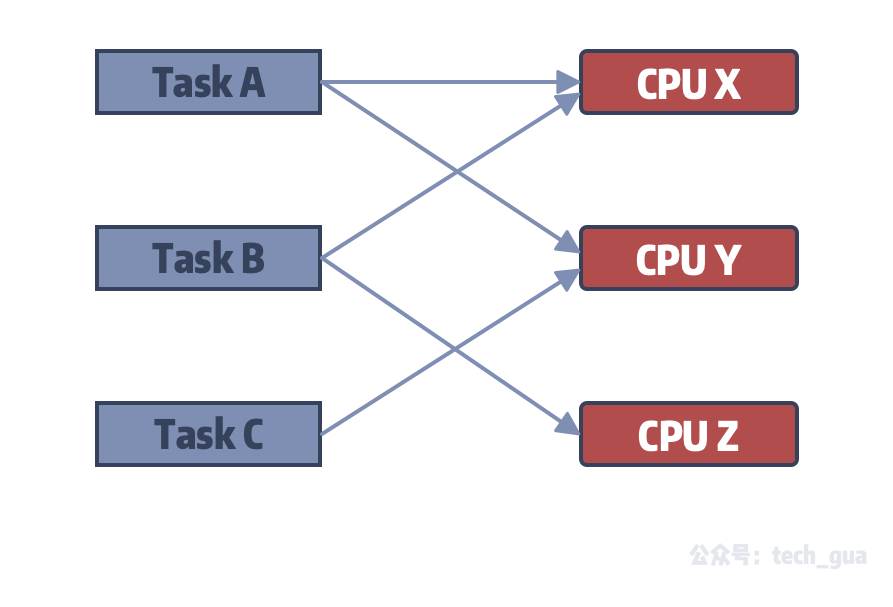



二分匹配的最大流思维 一瓜算法小册



二分图最大匹配 找老婆问题 确信 上地信息 Shangdixinxi Com
04 · 二分图(最大匹配,最小覆盖数,最大独立集合) 定义: 设G= (V, E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A , B),且图中的每条边(i, j)所关联的两个定点分别属于这两个不同的顶点集,则称图G为一个二分图。 性质: 定理:当且仅当无向 · 这篇文章讲无权二分图(unweighted bipartite graph)的最大匹配(maximum matching)和完美匹配(perfect matching),以及用于求解匹配的匈牙利算法(Hungarian Algorithm);不讲带权二分图的最佳匹配。 二分图:简单来说,如果图中点可以被分为两组,并且使得所有边都跨越组的边界,则这就是一个二分图。模板二分图最大匹配 题目描述 给定一个二分图,其左部点的个数为 $n$,右部点的个数为 $m$,边数为 $e$,求其最大匹配的边数。
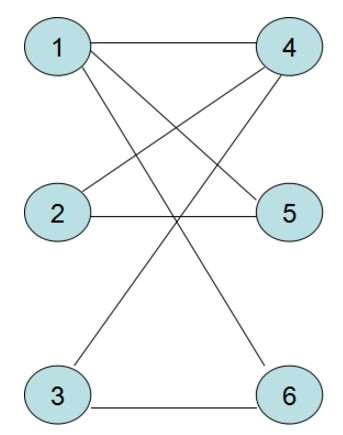



Bipartite Graph 二分图 Elmagnifico S Blog




二分图的最大匹配 匈牙利算法 简书
· 二分图最大匹配 洛谷 p5030长脖子鹿放置 相关推荐 网络流二分图最大流最大匹配 洛谷 P3355网络流24题骑士共存问题
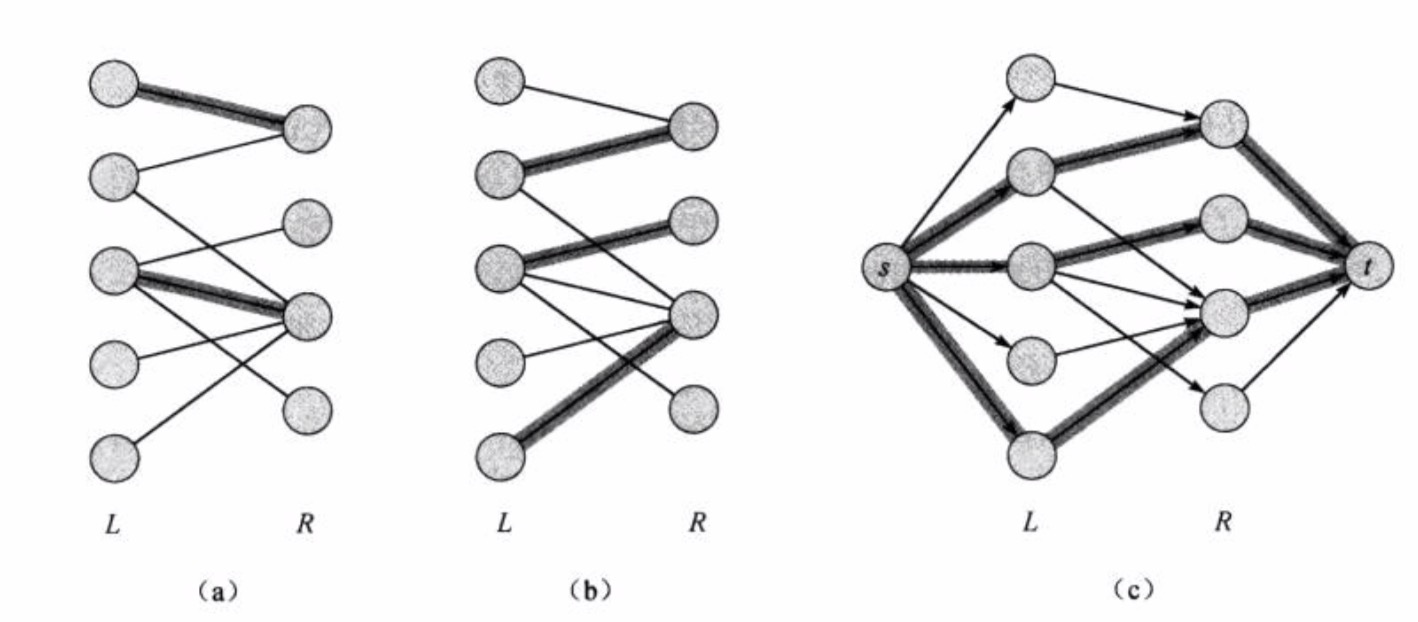



最大二分匹配与匈牙利算法 吾青




二分图 最大匹配 最小覆盖数 最大独立集合 牛客博客




二分图及其最大匹配 知乎




二分图匹配相关算法及例题分析最大匹配匈牙利算法最大权匹配km算法 二分图类型问题汇总 傻子是小傲娇的博客 大钊 程序员宅基地




二分图的最大匹配 匈牙利算法 简书




二分图匹配 最大匹配 匈牙利算法 摸鱼世界 摸鱼酱的个人博客




用于二分图匹配的匈牙利算法 Comzyh的博客




二分图最大匹配的一些证明 Five的博客 51cto博客




二分图匹配 最大匹配 匈牙利算法 摸鱼世界 摸鱼酱的个人博客




06 飞行员配对 二分图最大匹配 华为云




二分图最大匹配 匈牙利算法 Wenr 博客园



算法 二分图最大匹配 Mina




二分图 牛客博客



51nod 06 飞行员配对 二分图最大匹配 裸匈牙利算法求二分图最大匹配题 Ninding 博客园
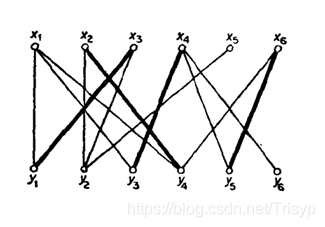



二分图匹配及匈牙利算法的全面讲解及python实现 Trisyp的博客 Csdn博客



二分图最大匹配 匈牙利算法 洛谷p71座位安排 哔哩哔哩 つロ干杯 Bilibili




二分图匹配 Ppt Download




Learning 二分图最大匹配的konig定理
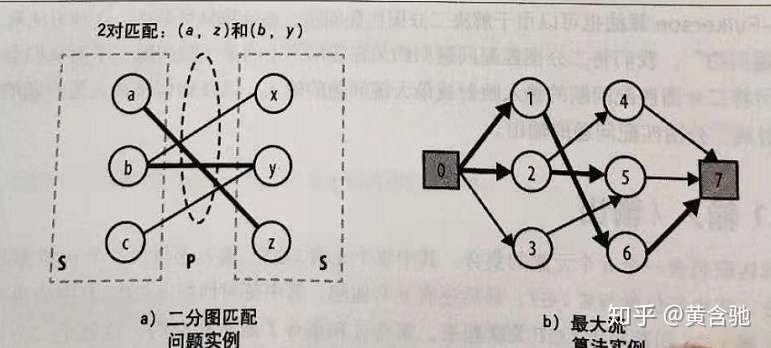



网络流算法学习笔记2 简洁易懂 二分图匹配求解算法 代码及算法设计一书关于二分图匹配章节的翻译 知乎




今際の国の呵呵君 Algorithm Maximum Matching Of Bipartite Graph 二分图的最大匹配



算法设计与分析 0016 二分图匹配问题 Gary Chan S Blog
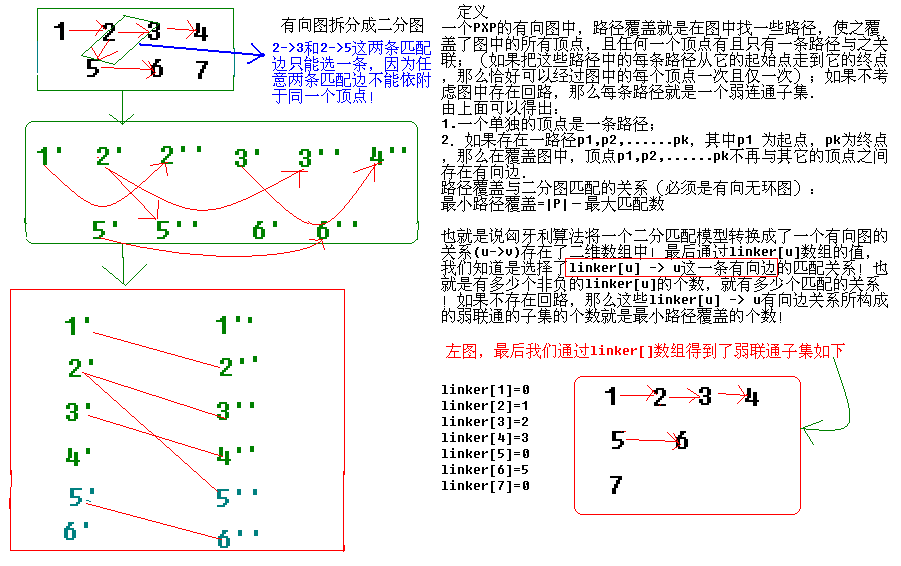



二分匹配最大匹配的理解 附图解 阿里云开发者社区
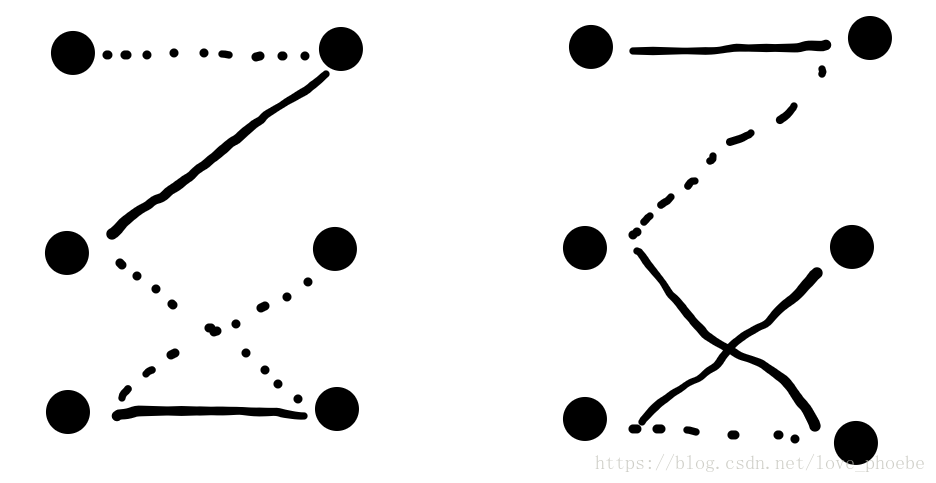



二分图匹配相关算法及例题分析最大匹配匈牙利算法最大权匹配km算法 二分图类型问题汇总 傻子是小傲娇的博客 大钊 程序员宅基地
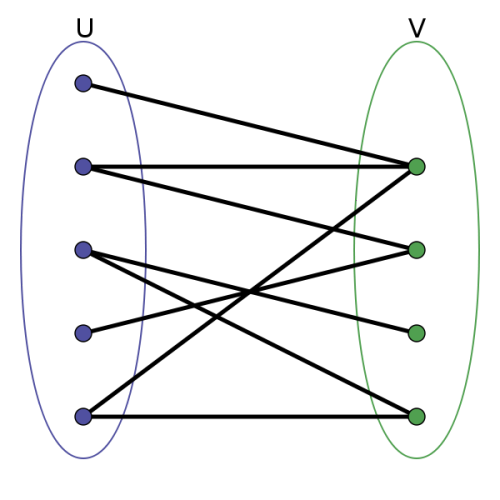



Poj 二分图的最大匹配 Bajiaoyu517的博客 Csdn博客




Poj 30 二分图最大匹配 华为云



蒟蒻图论 二分图匹配 蒟蒻のblog




算法导论 二分图最大匹配 简书



算法设计与分析 0016 二分图匹配问题 Gary Chan S Blog
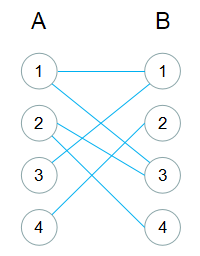



从二分图开始到最大匹配
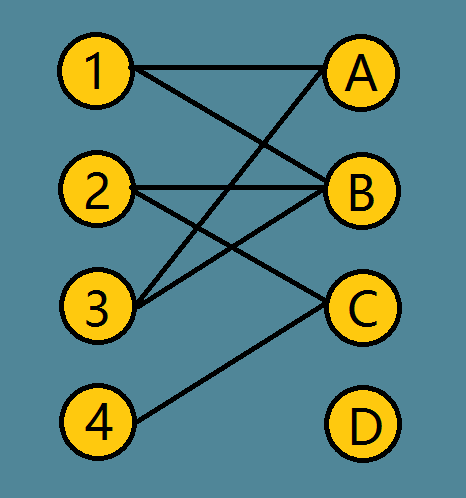



二分图匹配の匈牙利算法 银河渡舟 博客园
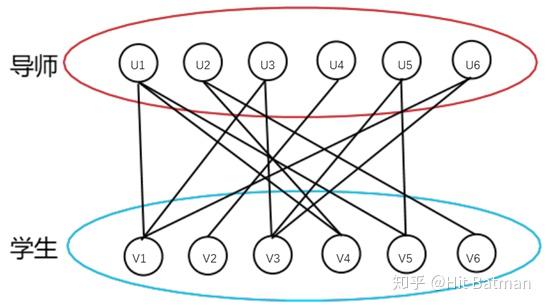



简单理解二分图与匈牙利算法 知乎




二分图匹配问题 模板 Acm Hades的博客 Csdn博客 二分图的匹配问题
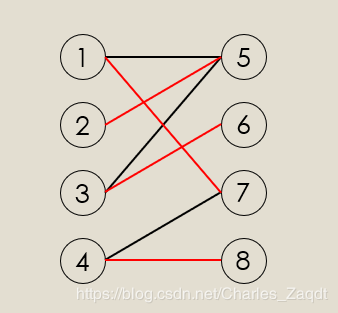



干货 二分图详解 知乎




匈牙利算法 二分图最大匹配问题 Mathor



蒟蒻图论 二分图匹配 蒟蒻のblog




二部图匹配 第1页 图说健康



二分图匹配与应用 哔哩哔哩 つロ干杯 Bilibili
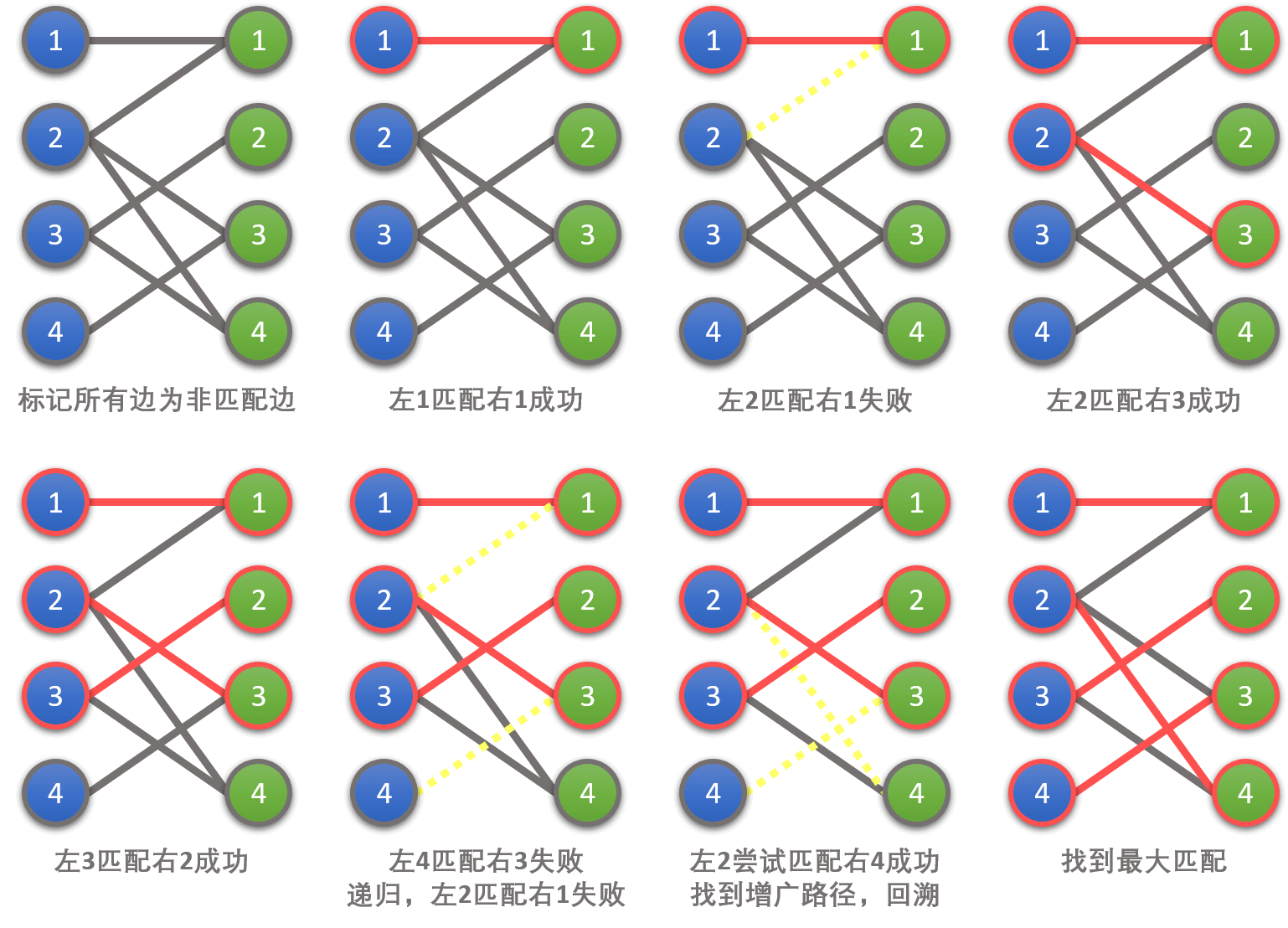



浅谈匈牙利算法




二分图最小覆盖数 最大匹配数 最大独立集 总数 最小覆盖集证明hdu 1068 Qzq 程序员宅基地 程序员宅基地




二分图最大匹配 最大流 Thinkspiritlab




二分图匹配问题 牛客博客



二分图匹配和匈牙利算法 简书




Acwing 861 二分图的最大匹配 匈牙利算法 云社区 华为云




二分图题型总结与模板 Acwing
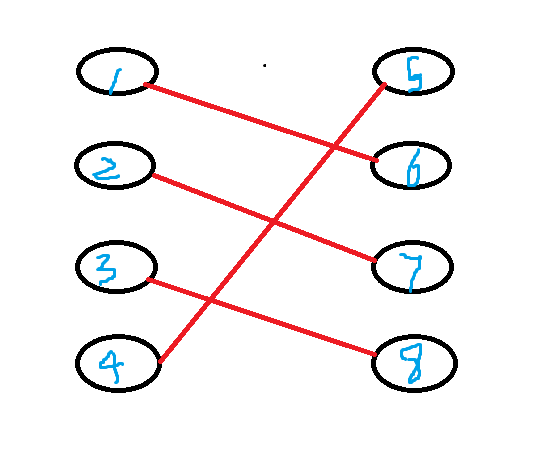



每日一侃 二分图最大匹配 匈牙利算法 Acwing
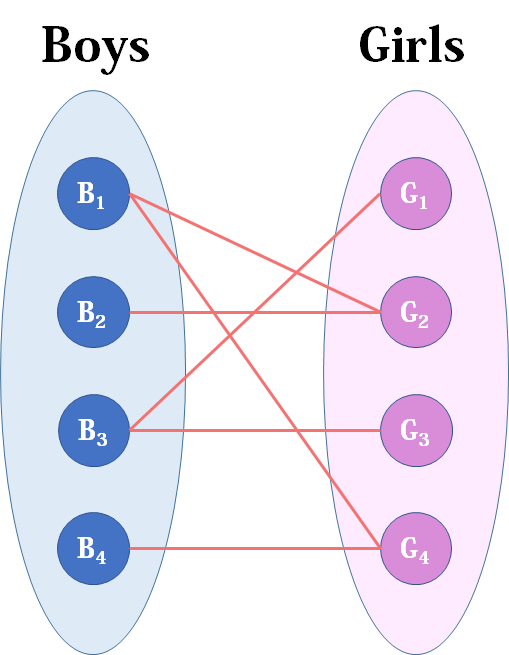



算法学习笔记 5 匈牙利算法 知乎
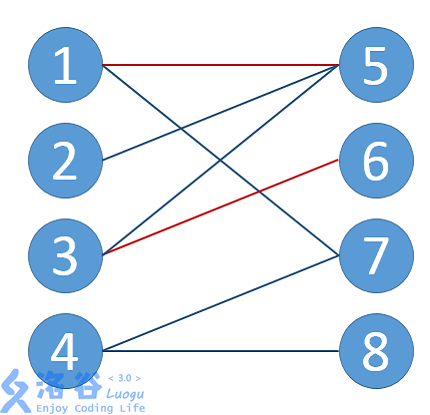



浅析二分图 最大匹配与最佳匹配 3 Soon 的博客 洛谷博客




06 飞行员配对 二分图最大匹配 华为云




Ppt 二分图匹配powerpoint Presentation Free Download Id




匈牙利算法 二分图最大匹配问题 Mathor
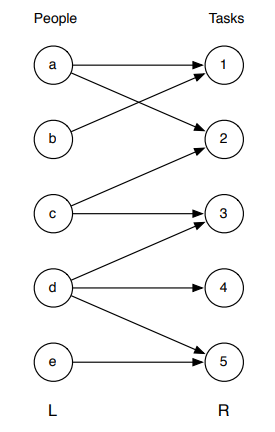



二分图 超详细 Coordinate
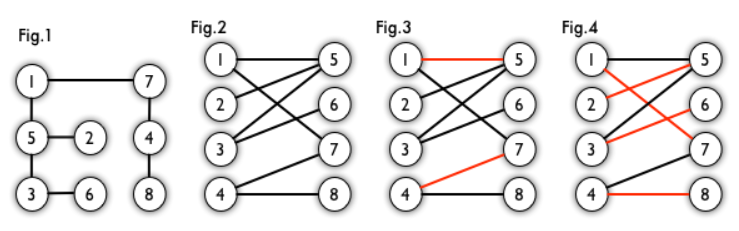



二分图的最大匹配 完美匹配和匈牙利算法 猪突猛进 博客园




求解分配问题 二 二分图最大匹配算法 Wangzhenyang2的博客 Csdn博客
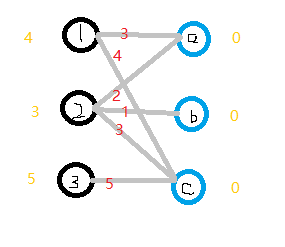



图论 二分图匹配基本算法之km算法解析 浅悠悠的个人博客




二分图的最大匹配 码农家园
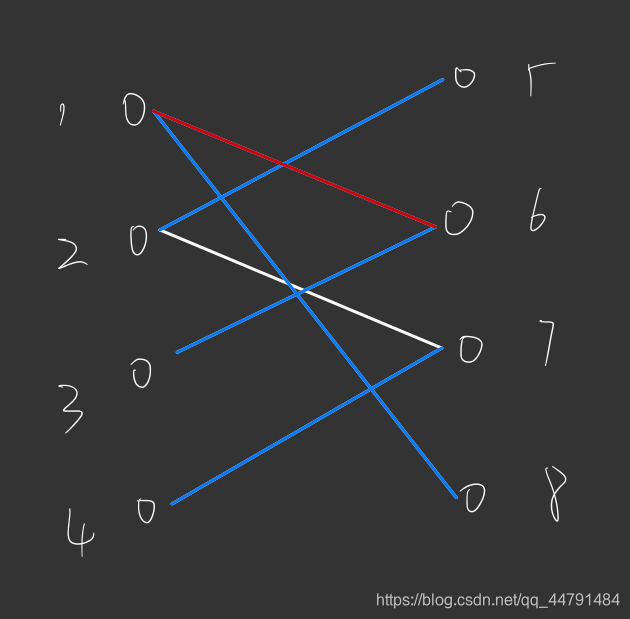



Acwing 861 二分图的最大匹配 匈牙利算法 云社区 华为云



算法设计与分析 0016 二分图匹配问题 Gary Chan S Blog



蒟蒻图论 二分图最大带权匹配 蒟蒻のblog



二分图最大匹配的konig定理及其证明 Matrix67 The Aha Moments




二分图匹配 搜狗百科




二分圖的最大匹配 匈牙利算法的思想 台部落




模板 二分图最大权完美匹配km算法




二分图最大匹配 简书



二分图的最大匹配 秋岛流云的个人空间 Oschina 中文开源技术交流社区




Zoj 39 Prime Set 匈牙利算法 二分图最大匹配 茄子min 博客园
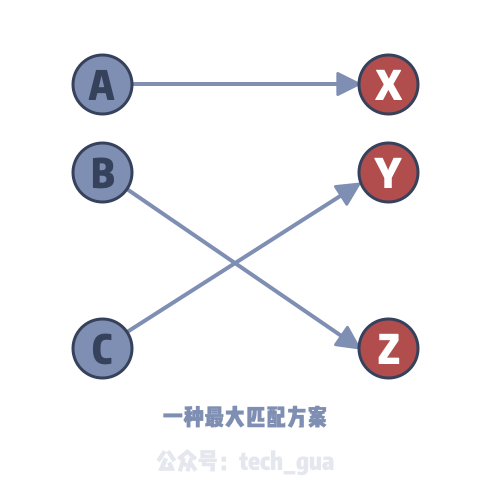



二分匹配的最大流思维 一瓜算法小册




二分图匹配匈牙利算法和km算法简介 Ppt Download




二分图最大匹配 U的专栏 Csdn博客
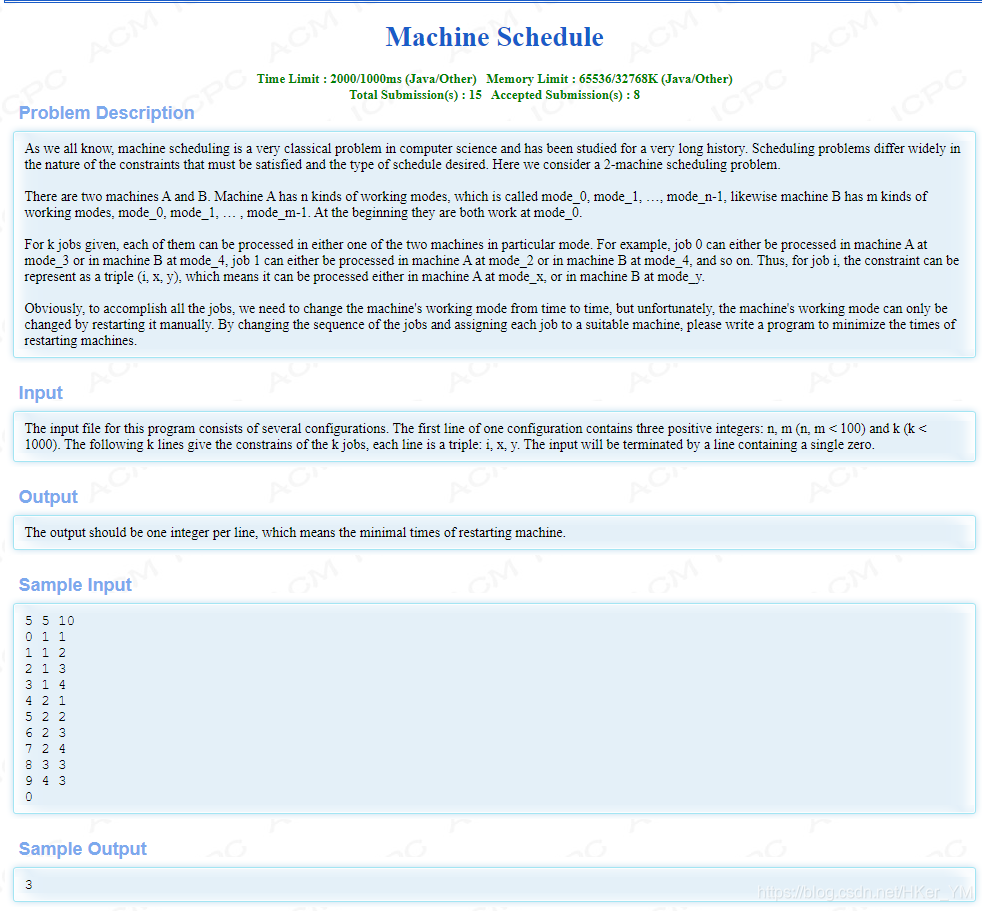



Machine Schedule Hdu 1150 二分图最大匹配 最小点覆盖 Hker Ym S Blog




二分图匹配 指派问题 Herongwei 的blog Csdn博客
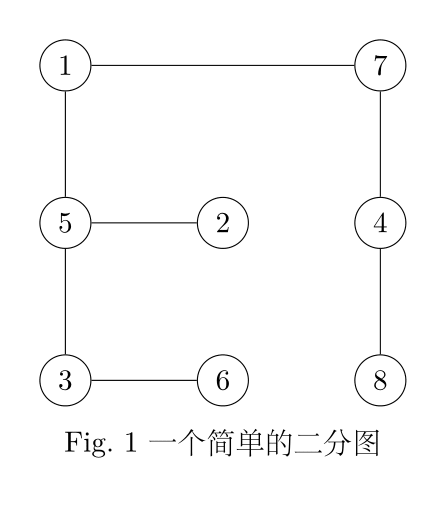



二分图最大匹配问题与匈牙利算法的核心思想 始终



二分图最大匹配问题 匈牙利算法 Liam S Blog




用于二分图匹配的匈牙利算法 Comzyh的博客




今際の国の呵呵君 Algorithm Maximum Matching Of Bipartite Graph 二分图的最大匹配




二分图匹配之最佳匹配 Km算法 Lanly 博客园




通俗易懂小白入门 二分图最大匹配 匈牙利算法
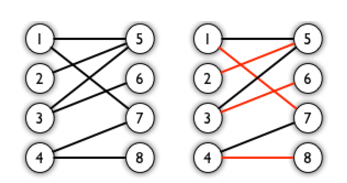



Bipartite Graph 二分图 Elmagnifico S Blog




极简数据结构16 二分图 我会反转二叉树



蒟蒻图论 二分图匹配 蒟蒻のblog



算法设计与分析 0016 二分图匹配问题 Gary Chan S Blog



Rocky 二分图 最大匹配 Dinic C 竞赛级入门第三十五节 哔哩哔哩 つロ干杯 Bilibili
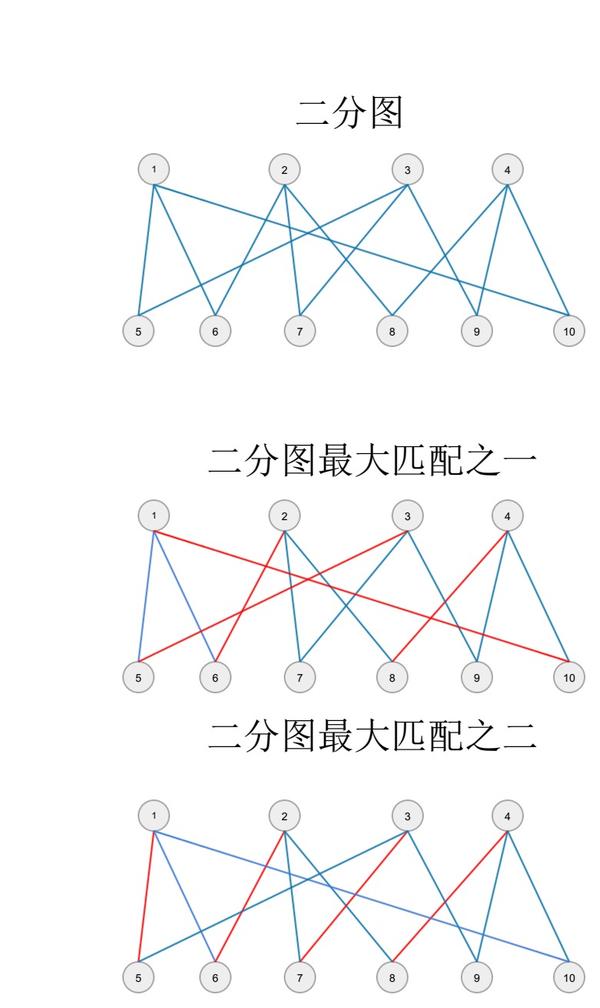



如何寻找一个二分图所有最大匹配 Nui Dx 的回答 知乎
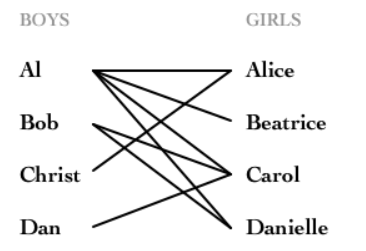



二分图的最大匹配 完美匹配和匈牙利算法 猪突猛进 博客园



二分图的最大匹配 最小顶点覆盖 最大独立集等价的线性规划证明 知乎



0 件のコメント:
コメントを投稿